Ampère's law

Ampère's law is a law that is part of Maxwell's 4 equations, it replaced Biot Savart's law. This law allows us to calculate the magnetic field by means of electric currents. The law was discovered in 1826 by André Marie Ampère and connects the electric current intensity and the magnetic field it produces.

Unlike electric fields, magnetic field lines are not conservative, in other words, the circulation in a closed line is not zero. If the direction in which the currents circulate has the same direction as the direction of the surface vector, it will be positive. On the other hand, it will be considered negative if the direction is opposite.

Formula to know the magnetic field

Ampère's law allows us to know the magnetic field produced by the current by applying the following formula.

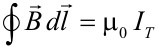
On the one hand, the first integral, that is to say, the left-hand part of the formula represents the circulation found in the field lines in their closed path. In addition, the dl refers to the tangent vector of the selected path at each point. On the other hand, the right-hand side of the formula refers to:

• μ0 = permeability found in a vacuum
• IT= the net current intensity

Maxwell later corrected Ampère's law, realizing that magnetic fields, like electric currents, change with time. So the updated formula reads as follows:

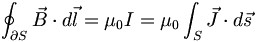
J= charge current

dS= vector perpendicular to the surface at every point

Applications of Ampère's law

Ampère's law allows us to know the magnetic field of:

• A conducting wire

• A cylindrical wire of radius

• A solenoid

This law can be used for electromagnets, generators, transformers, and motors.

Applications for a solenoid

The law discovered by André Marie Ampère can be applied to a solenoid in order to find the magnetic field inside it. This magnetic field is proportional to the current applied and to the number of turns per its length. The electromagnet is an application where we can clearly see this law since the magnetic field is equal to the sum of the magnetic fields of this spiral and this can be calculated with Ampère's law.

In addition to applying it to solenoids, it can also be applied to toroids.