Induced magnetism

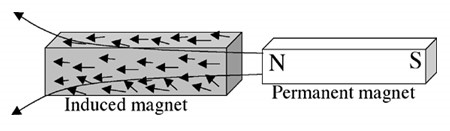
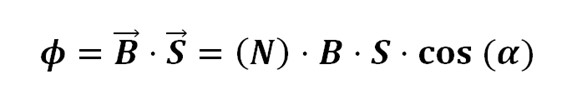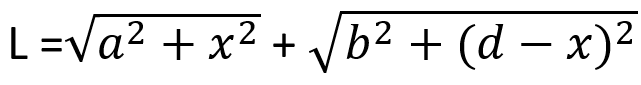Induced magnetism is a non-magnetized magnetic material coming into contact with a pole of a permanent magnet. Consequently, the unmagnetized material becomes a magnet. As soon as the magnetic field disappears, the magnetism of the magnet is lost. Induced magnetism is known because magnetism is induced in material that lacks magnetism.

The magnetic domains inside are aligned for a moment in the direction of a magnetic field external to them.

The induced magnetization is proportional to the magnetic field strength of the magnet inducing the magnetism, i.e. the stronger the original field strength, the more magnetization is induced.

The magnetic field strength can be known from Faraday's law.

Magnetic induction is the measure of the concentration of the magnetic flux. Magnetic flux is the number of magnetic field lines on a surface. To obtain the magnetic induction we must apply the following formulae:

• In the case of a magnetic medium:

B = µ-H

• - In the case of a vacuum:

B₀ = H

To know the magnetic flux we must apply:

Φ = magnetic flux

B = magnetic field in Tesla

S = surface area

Induced magnets

Induced magnets are elements that possess induced magnetism. Temporary or induced magnets are made of soft magnetic materials such as iron, cobalt, and nickel. Temporary or induced magnets can be magnetized and demagnetized, a basic example being an electromagnet or coil. The induced current is the current type of electromagnetic induction. This happens when an electric current, by changing its potential from its polarity

Difference between an induced magnet and a permanent magnet

On the one hand, an induced magnet is a temporary magnet that can only hold a magnetic charge for a moment after it has been subjected to a magnetic force. On the other hand, a permanent magnet always holds its charge and never loses it.

The most common examples of induced magnetism are:

• Paper clips
• Electric batteries
• Generators
• Transformers

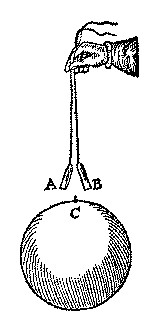
Gilbert's experiment and induced magnetism

Gilbert placed two parallel bars of iron on a sphere through chains. Observing it, he noticed that the two bars repelled each other.

The classical free-electron model

The classical free-electron model consists of metal atoms arranged in a crystalline structure that can vibrate. This electron has a gas-like perception of electrons. Unlike ordinary gas molecules. This type of electron is so-called because they have free charges.

The velocity of the free electron is 0 and it encounters the absence of the electric field. As soon as an electric field appears, the free electrons move toward the positive potential.

This theory explains why metals can conduct electricity. In this theory more than half of the elements found in the periodic table are metals.

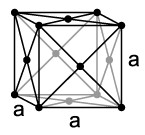
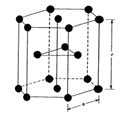
Type of structure:

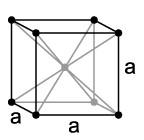
The free electron model is to show the behavior of valence electrons in a crystal structure of the solid metal. We can find 3 crystal structures:

- BCC → Centred cubic lattice, the atoms are located at the vertices in the middle of the cube.

- FCC → Cubic lattice with centered faces, the atoms are located at the vertices and on the faces of the cube.

- HCP → Compact hexagonal lattice, unlike the previous ones, this one is located at the vertex of a hexagonal prism, as we can see in the following image:

Tipos de modelos y teorías

In the classical model of free electrons we can find several models that form it:

- Drude's model → Between impacts, electrons make a free motion with the absence of relating to other electromagnets. The approach of the electromagnets independently is also known as free electrons.

- The Sommerfeld model → In this model we find that the electrons have no relationship to the atomic nuclei, being electrons similar to free particles.

There are 3 free electron theories:

1. Classical free electron theory = this theory was the first in 1900 and the one containing free electrons that are responsible for electrical conductivity.

2. Quantum free-electron theory = building on the previous theory, this theory created in 1928 states that electrons move freely with a constant potential.

3. Zone theory = here we find that the potential is in proportion to three. This theory is known as the band theory of solids.

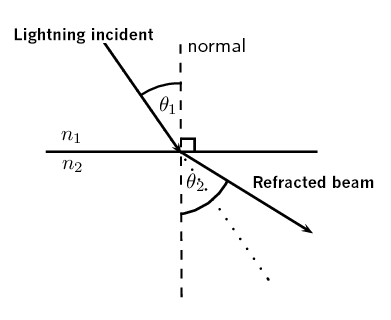
Snell's law

This law was discovered by Willebrord Snell Van Royen in 1621 and is intended to know the angle of refraction of light as it passes through a surface with a different refractive index.

Snell's law can also be seen as the law of refraction of light and Fermat's principle, this law states that the connection that has the sines of the angles that are in refraction is the same as the inverse ratio of the indices that has the refraction within the media.

Fermat's principle can lead to the law of refraction, which states that light travels between two points in the shortest possible time.

Snell's law is the law that establishes the connection between the angle of incident light and the angle of transmitted light.

How does Snell's law relate to magnetism?

Snell's law connects the angle of refraction of light passes through the separation found in two different media both in the propagation of light and in an electromagnetic wave.

Below, we can see a table of the cooling rates of some substances.

It is related to the refraction of waves.

Snell's Law Formula

The following formula means that the angle of reflection is equal to the angle of incidence.

n1- sinθ1=n2 - sinθ2

n1 = refractive index of the first medium

n2 = refractive index of the second medium

sin = trigonometric function of sine

θ1 = angle of incidence of the light beam

θ2 = exit angle of the light beam

In the case where n1 >n2 andsinθ1> sinθ2 e the refracted index approaches the normal.

In the case where n1 ​ sinθ1 ​sinθ2​ ​ e the refracted index moves away from the normal.

The proof of Snell's law can be obtained from Fermat's principle. To derive the law of reflection to Fermat's principle, one needs to know the path length from A to B:

Snell's law establishes the relationship between a ray of light crossing the boundary or surface of separation between 2 substances lying side by side and the corresponding refractive index.

Applications of the law of refraction

The application of this law allows us to have prisms, among other things. Without this bending of light, we would not be able to focus our retina.

Some examples of Snell's law are the reflection of the field in the water of the lake. Another clear example of this law is the optical fiber which is used in data networks.