Gauss's law

Gauss's law or also known as Gauss's theorem was discovered by Karl Friederich Gauss, a mathematician who formulated in 1835 the relationship found between the electric flux circulating on a closed surface which has an electric charge. It was not until 1869 that it was published.

Gauss's law states that the electric field flux found on the closed surface is the same between the charge inside the surface and the permeability of the vacuum.

What are the properties of Gauss's law?

The properties of Gauss's law:

- The electric flux is directly proportional to the net charge of the closed surface.

- However irregular the electric flux is, it is independent of the shape of the surface.

- This electric flux does not depend on how the charge inside the surface in question is distributed.

- The number of lines passing through the surface is 0, so the external charges contribute nothing to the electric flux.

The formula for Gauss's law is?

To obtain the total electric charge we need to use the following formula

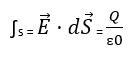
The vector of E = electric field

d together with the vector of S_. = surface vector

Q = charge

_ɛ0= permeability of the vacuum, 8.85pFm^-1

In addition to this formula, we can find it by the differential formula. This differential formula is obtained from the divergence theorem.

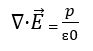
p= volume charge density

∇ = divergence

As mentioned above, the flux of the electric field on a closed surface is proportional to its charge.

The law in the form of a sphere

To obtain the magnetic field that a sphere possesses, we must use Gauss's law. This law shows us that the electric field that the sphere has is equal to the magnitude regardless of where it is on the surface.

Unlike the normal Gauss's law, when we are applying it to a sphere, to find out the magnetic field that a sphere has, we only have to multiply the magnetic field strength (the one that is on the surface of the sphere) and multiply it by the area of its surface, obtaining the following formula:

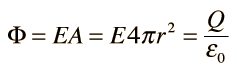
To obtain the electric field at the radius, it must be obtained using the following formula:

On the other hand, when we want to apply another charge, we must add it to the upper part by multiplying the other in the upper part of the formula.